Fazendo um pouco melhor (ainda a provinha do GDD)
Ainda não desisti de resolver a prova do GDD em Erlang. Não. Não preciso resolver em Erlang, mas, com tanta gente usando Java, PHP e até PL/SQL pra resolvê-la (e com um amigo que usou Haskell), eu fiquei com vontade.
Também posso repetir uma do ano passado e fazê-la em Lisp.
Então. Erlang é avessa a loops. Loops fazem coisas mudarem de estado e linguagens funcionais não gostam que coisas mudem de estado. O dialeto de Lisp que eu usei ano passado também, mas faz uma concessão e me deixa fazê-los.
O comparador
Assim, a nossa primeira função com loop da prova, cmp_goog, que é assim:
def cmp_googlon(p1, p2): v = 'jgptzmqskbclrhdfnvwx' for l1, l2 in zip(p1, p2): if v.index(l1) != v.index(l2): return v.index(l1) - v.index(l2) return len(p1) - len(p2)
Ficaria assim:
def cmp_googlon(p1, p2): v = 'jgptzmqskbclrhdfnvwx' if p1 == p2: return 0 elif len(p1) == 0 or len(p2) == 0: return len(p1) - len(p2) elif p1[0] == p2[0]: return cmp_googlon(p1[1:], p2[1:]) else: return v.index(p1[0]) - v.index(p2[0])
Note que, em vez de comparar as strings em um loop, eu comparo só seus primeiros elementos e, se os dois forem iguais, eu chamo o comparador de novo, agora com as strings sem a primeira posição.
Bases numéricas
A outra função serve para nos dar o valor em base 10 de um número em googlon. O original é um clássico, em que você percorre os dígitos do número e vai totalizando os valores de cada casa:
def valor_numerico(p): v = 'jgptzmqskbclrhdfnvwx' vn = 0 i = 0 for c in p: vn += v.index(c) * (20 ** i) i += 1 return vn
A idéia é que o valor de um número é o valor do seu dígito menos significativo somado ao produto da base multiplicada pelo valor do resto. No caso de números em base 10, 123 é dado pela soma de 3 com o produto de 10 e 12, sendo que 12 é dado por 2 somado a 10 vezes 1. Transcrito em Python, a nova versão é bem mais concisa:
def valor_numerico_f(p): v = 'jgptzmqskbclrhdfnvwx' if len(p) == 1: return v.index(p) else: return v.index(p[0]) + 20 * valor_numerico_f(p[1:])
Agora eu preciso de algumas horas para escrever a versão em Erlang. Desejem-me sorte.
Solução para a provinha do Google Developer Day 2011 em Python
Esse ano, resolvi tratar com um pouco mais de respeito a prova do GDD. Ano passado, eu resolvi com o prompt do Python aberto, olhando o browser em uma janela e o prompt na outra. Esse ano, as perguntas eram um pouco mais trabalhosas e as strings maiores e isso me fez, em vez disso, escrever um programa. Mais tarde eu coloco o programa no github, mas, por hora, eu transcrevo e comento aqui a minha solução.
A prova apresenta dois textos escritos no idioma Googlon, com os quais vamos trabalhar, e quatro perguntas. Para ajudar (eles são realmente bonzinhos), eles dão as soluções para o primeiro texto, o que ajuda a testar se o código está correto.
Letras foo, bar e preposições
A primeira pergunta explica que algumas letras são chamadas de "letras foo" e todas as demais, "letras bar" e que preposições são palavras de cinco letras que começam com uma letra bar e não contém a letra "q" (é muito provável que a sua prova seja diferente da minha e que elas sejam geradas aleatoriamente - é como eu faria). Para ajudar a resolver, eu escrevi algumas funções
def foo(l):
return l in "snrbg"
def bar(l):
return not foo(l)
def preposicao(p):
return len(p) == 5 and bar(p[-1]) and 'q' not in p
Aí, testar a resposta dada no enunciado é fácil:
>>> palavras_a = texto_a.split(' ')
>>> len(filter(preposicao, palavras_a))
63
Assim como responder a pergunta:
>>> palavras_b= texto_b.split(' ')
>>> len(filter(preposicao, palavras_b))
57
Verbos e verbos em primeira pessoa
A segunda pergunta ensina que verbos são palavras de 6 letras que terminam em uma letra bar. Se ele também começar com uma letra bar, estará em primeira pessoa.
def verbo(p): return len(p) >= 6 and bar(p[-1]) def verbo_primeira_pessoa(p): return verbo(p) and bar(p[0])
Agora podemos testar nosso código com o dado do enunciado:
>>> len(filter(verbo, palavras_a)) == 216 True >>> len(filter(verbo_primeira_pessoa, palavras_a)) == 160 True
E descobrir a nossa própria resposta:
>>> len(filter(verbo, palavras_b)) 224 >>> len(filter(verbo_primeira_pessoa, palavras_b)) 154
No meu caso, eu tinha 224 verbos, dos quais 154 em primeira pessoa.
Vocabulário
Agora o problema pede para criar uma lista com o vocabulário, ordenado segundo o alfabeto googlon. Para isso, eu vou usar o ordenador que já vem embutido nas listas do Python e vou produzir uma função de comparação. Essa função pode ser facilmente plugada em seu próprio sort, se você quiser muito:
def cmp_googlon(p1, p2): v = 'jgptzmqskbclrhdfnvwx' for l1, l2 in zip(p1, p2): if v.index(l1) != v.index(l2): return v.index(l1) - v.index(l2) return len(p1) - len(p2)
E podemos testar com os dados do enunciado:
>>> vocabulario_a_unsorted = list(set(palavras_a)) >>> ' '.join(sorted(vocabulario_a_unsorted, ... cmp = cmp_googlon)) == vocabulario_a True
Nota: ao construir um set com as palavras do texto A, eu eliminei as repetições. Como objetos do tipo set não são ordenáveis, eu transformei o conjunto em uma lista.
Agora podemos encontrar nossa resposta:
>>> vocabulario_b_unsorted = list(set(palavras_b)) >>> vocabulario_b = ' '.join(sorted(vocabulario_b_unsorted, cmp = cmp_googlon)) >>> vocabulario_b 'jgspd jgv jpgzkx jzvjw jmrmlq jmdxx jmntpzq jqw jspk jkc jbb jcphbk jch jcv jlkm...
Números
Agora a prova nos explica que todas as palavras em googlon tem um valor numérico. Em googlon, os números são escritos do dígito menos significativo para o mais significativo e em base 20. Pra isso, precisamos de mais uma função:
def valor_numerico(p): v = 'jgptzmqskbclrhdfnvwx' vn = 0 i = 0 for c in p: vn += v.index(c) * (20 ** i) i += 1 return vn
que, podemos testar contra o enunciado:
>>> valor_numerico('blsmgpz') == 262603029
True
Essa parte está certa. Mas a pergunta pede para contarmos os números bonitos. Para eles, números bonitos são divisíveis por 5 e maiores que 492528.
def numero_bonito(p): return valor_numerico(p) > 492528 and (valor_numerico(p) % 5 == 0)
Agora podemos testar:
>>> len(filter(numero_bonito, vocabulario_a.split(' '))) == 75
True
E chegar na nossa resposta:
>>> len(filter(numero_bonito, vocabulario_b.split(' ')))
71
Conclusão
Foi difícil? Nem um pouco. Se você não conseguiu responder por conta própria, precisa estudar mais. Foi mais trabalhosa do que a do ano passado? Um pouco. Por outro lado, ela tinha informações suficientes para você poder testar suas próprias soluções - e isso ajudou quem teve mais problemas para resolver a prova a aprender alguma coisa. Prova boa é assim - você aprende enquanto faz.
Uma última observação: eu gosto de list comprehensions, mas também gosto de map, filter e reduce. O código fica mais limpo quando eles são bem empregados.
Sobre a provinha do Google Developer Day 2011
Ano passado, quando a Google abriu as inscrições para o GDD, eu escrevi o primeiro de uma série de três artigos sobre a tal provinha. Esperei até o final das inscrições (e o sinal verde de um amigo que trabalha lá) para publicá-lo.
Não vou fazer diferente esse ano. Se você veio aqui querendo ver a solução dos problemas do ano passado, eles estão relacionados abaixo. Se, por outro lado, chegou aqui procurando um jeito fácil de entrar no evento, devia ter vergonha. Eu respeito a decisão da Google de usar a prova como uma forma de garantir que a platéia tenha melhores chances de entender o que o palestrante vai falar e não vou ajudar a estragar o processo de seleção de convidados deles. Quando as inscrições estiverem encerradas, eu volto aqui e publico a minha solução e aí você pode comparar com a sua.
De resto, boa sorte. A prova não é difícil e eu tenho certeza que você consegue. Você já chegou até aqui, afinal.
Um abraço e até lá.
Nota: Se você colocar aqui um comentário mostrando uma solução antes que sejam fechadas as inscrições, eu vou apagar pela mesma razão que me fez não publicar a minha ainda. Se você tem uma solução, volte depois.
Outra nota: Agora, que as inscrições estão encerradas, você pode achar soluções procurando no Google. Uma delas (em Java) foi postada em um comentário aqui. A mihha em Python está aqui. Há outras, algumas com escolhas de linguagem ainda mais estranhas do que a minha versão para computadores de 8-bits do ano passado. Acho uma pena que tantos tenham praticado GDD (Google-Driven Development, pun intended) e tenham googlado por respostas em vez de aprender a programar.
A provinha do GDD, em BASIC (para micros de 8 bits)
Eu confesso que me diverti resolvendo a provinha do GDD. Pra quem chegou agora, foi um teste aplicado pelo pessoal da Google para filtrar inscritos no Google Developer Day. Como eles tiveram muito mais inscritos do que espaço físico comportava, fazia sentido. Embora muitos tenham reclamado, era uma prova muito simples e eu resolvi usando duas linguagens diferentes, Python e Clojure, ambas modernas.
BASIC?!
Um passatempo meu é em paleocomputação, em particular computadores obsoletos, daquelas famílias que não deixaram descendentes diretos. Eu coleciono e, quando possível, restauro, computadores antigos - se você tiver um desses, a propósito, aceito doações. Por isso, eu resolvi brincar um pouco e resolver a provinha do GDD usando um TRS-80 Model III e um Apple II (um //e enhanced, para ser mais preciso). Para tornar a minha vida mais fácil (e evitar um divórcio) eu usei emuladores em vez de computadores reais. Com isso eu pude escrever o código usando um editor de textos de verdade e "colá-lo" no emulador. Em ambas as plataformas, usei seus interpretadores BASIC embutidos na ROM.
Um outro motivo é por esse dialeto de BASIC ser uma linguagem muito mais simples e pobre de recursos do que as duas outras que eu usei nessa brincadeira. Essa simplicidade é visível nas construções que aparecem nesses programas. É interessante notar como os mecanismos de controle de fluxo do programa são mínimos e se mapeiam quase que diretamente ao que o processador entende.
O emulador
A história do emulador é, por si, interessante. Para os dois eu usei o MESS. MESS é uma derivação do MAME que pretende replicar, da forma mais precisa possível, computadores obsoletos. Como os pacotes do Ubuntu me deram algumas dores-de-cabeça, eu compilei a versão mais nova do MESS. Não é difícil e o pessoal do IRC (#messdev na EFNet) foi mais do que gentil e eu teria apanhado muito mais sem eles.
Aliás, quanto a essa coisa de IRC, se vocë desenvolve software e não usa, devia usar. IRC é como um monte de projetos são coordenados, reuniões são feitas e dúvidas tiradas. É normalmente mais rápido que listas de discussão e fórums web. Ache velho e feio por sua conta e risco. Eu não levo a sério nenhum projeto de software aberto que não tenha um canal de IRC com desenvolvedores e usuários conversando.
Mas vamos aos problemas, que são o mais interessante
1) O que esse programa faz?
x = 7 y = 4 if y > 2, then y = y * 2 else x = x * 2 print (x + y)
Em um TRS-80, faríamos assim:
10 X = 7 20 Y = 4 30 IF Y > 2 THEN Y= Y * 2 ELSE X= X * 2 40 PRINT X + Y
Mas isso seria uma estupidez. BASIC (aquele dos anos 70 e 80, pelo menos) é um ambiente interativo - você pode testar idéias de forma rápida e fácil, sem escrever programas. Um programador dos anos 80 faria assim:
X = 7 Y = 4 IF Y > 2 THEN Y= Y * 2 ELSE X= X * 2 PRINT X + Y
E, no seu TRS-80, veria isso:

Em um Apple II, por conta do BASIC não ter a palavra ELSE, teríamos que fazer um pouco diferente:
X = 7 Y = 4 IF Y > 2 THEN Y= Y * 2 IF Y <= 2 THEN X= X * 2 PRINT X + Y
E veria algo como

Em forma de programa, no Apple II (e em qualquer caso em que precisássemos de um IF/THEN/ELSE multi-linhas), o jeito típico seria usar um GOTO:
10 X = 7 20 Y = 4 30 IF Y > 2 THEN Y= Y * 2 : GOTO 50 40 X= X * 2 50 PRINT X + Y
E teríamos isso:

Como a versão BASIC disse "15" e concordou com as versões Python e Lisp, eu me dou por satisfeito.
2) Quantas vezes esse programa imprime "hello"?
for i = 1 to 5
if i != 2, then
for j = 1 to 9
print 'hello'
O programa ficaria assim:
10 FOR I = 1 TO 5 20 IF I <> 2 THEN FOR J = 1 TO 9: PRINT "hello": NEXT 30 NEXT
Sorte nossa o FOR J caber em uma linha.
Ainda assim, estamos com o mesmo problema que tivemos na nossa primeira tentativa (no original em Python) - que é nos obrigar a contar. Um jeito um pouco melhor ficaria assim:
10 FOR I = 1 TO 5 20 IF I <> 2 THEN FOR J = 1 TO 9: C = C + 1 : PRINT C, "hello": NEXT 30 NEXT
Alguém pode perguntar: "Qual é o valor inicial de C?". No BASIC daquele tempo variáveis do BASIC são tipadas pelo nome ("C" só pode representar um número real) e variáveis não inicializadas são zero ou, no caso de strings ("C$", por exemplo) strings vazias. Ou seja, assim que o programa começa a rodar, C é zero - e podemos contar com isso.
Se estiver incomodando muito, mas muito mesmo, digite "5 C = 0" e seja feliz. Não vai fazer mal.
Se fizermos isso no TRS-80, ficaremos com algo assim:


De novo, podemos ficar felizes. O programa em BASIC concorda com os outros - temos 36 (que é a resposta certa, afinal).
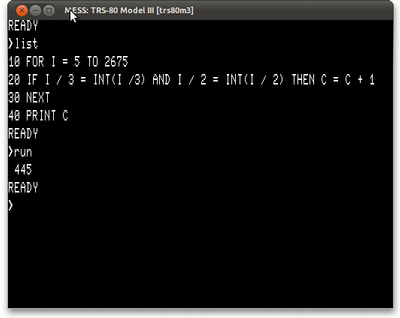
3) Quais números, entre 5 e 2675 são pares e divisíveis por 3?
Aqui estamos tão mal quanto o pessoal que fez com Java. Não dá pra fazer nada tão conciso quanto os exemplos em Python e em Clojure. BASIC não tem nenhuma das funcionalidades de geradores de listas que Ruby, Python, Clojure e qualquer linguagem moderna tem.
10 FOR I = 5 TO 2675 20 IF I / 3 = INT(I /3) AND I / 2 = INT(I / 2) THEN C = C + 1 30 NEXT 40 PRINT C
Quando rodar, o programa vai dizer que há 445 números assim.
4) Números bonitos
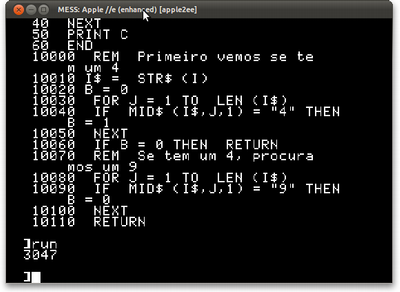
A pergunta nos apresenta Barbara e seus critérios para que números sejam ou não bonitos. Para ela, números são bonitos se contiverem um dígito 4 e não contiverem um dígito 9. Ao final, nos pergunta quais números entre 14063 e 24779, inclusive, são bonitos.
Esse fica mais complicado. O BASIC que vinha nesses computadores era limitado e não permitia que o programador definisse funções além do mais trivial (uma linha, sem condições). Vamos, por isso, usar uma técnica há muito esquecida (ou que deveria ter sido) que é passar informações por meio de variáveis globais. No caso dos nossos interpretadores, todas as variáveis são globais. Mesmo quem programa em assembly pode contar com a pilha nessas horas. Em BASIC, nem isso.
Você leu direito. Programar naquele tempo não era fácil.
O esqueleto do programa fica assim:
10 FOR I = 14063 TO 24779 20 GOSUB 10000 30 IF B = 1 THEN C = C + 1 40 NEXT 50 PRINT C 60 END
Mas ainda falta o trecho que começa em 10000 que, você deve ter adivinhado, diz se o I é um número bonito e devolve um 1 em B se ele for. O que você vai ver não é bonito para nenhum valor de I, portanto, prepare-se:
10000 REM Primeiro vemos se tem um 4 10010 I$ = STR$(I) 10020 B = 0 10030 FOR J = 1 TO LEN(I$) 10040 IF MID$(I$, J, 1) = "4" THEN B = 1 10050 NEXT 10060 IF B = 0 THEN RETURN 10070 REM Se tem um 4, procuramos um 9 10080 FOR J = 1 TO LEN(I$) 10090 IF MID$(I$, J, 1) = "9" THEN B = 0 10100 NEXT 10110 RETURN
Após um longo tempo, seu computador vai dizer que são 3047 números bonitos:
Nesse ponto, estou começando a achar que eu era mais inteligente nos anos 80. O malabarismo mental de lembrar que variável guarda o que e em que partes do programa essas coisas são alteradas é complicado. E é um bom exercício.
5) Os telefones
A última pergunta nos apresenta um país em que os números de telefone têm 6 dígitos. Números não podem ter dois dígitos consecutivos idênticos, porque isso é caído. A soma dos dígitos tem de ser par, porque isso é legal e o último dígito não pode ser igual ao primeiro, porque isso dá azar.
Vamos começar pelas sub-rotinas. A primeira, para ver se o número de telefone é caído:
10000 REM ve se N$ e caido. Se for, C = 1 10010 C = 0 10020 FOR J = 1 TO LEN(N$) -1 10030 IF MID$(N$, J, 1) = MID$(N$, J + 1, 1) THEN C = 1 10040 NEXT 10050 RETURN
Depois, vendo se ele dá azar:
11000 REM se N$ der azar, A = 1 10010 A = 0 10020 IF LEFT$(N$, 1) = RIGHT$(N$, 1) THEN A = 1 10030 RETURN
E, por fim, se ele é legal:
12000 REM se N$ for legal, L = 1 12010 L = 0: S = 0 12020 FOR J = 1 TO LEN(N$) 12030 S = S + VAL(MID$(N$, J, 1)) 12040 NEXT 12050 IF S / 2 = INT(S / 2) THEN L = 1 12060 RETURN
Vale a pena notar um padrão - como todas as variáveis são globais, é preciso tomar cuidado para que um pedaço do programa não estrague o outro. Nessas subrotinas meu habitual "FOR I" passou a ser "FOR J" para que meu loop da sub-rotina não estrague o loop principal. Eu podia também ter reutilizado o L como acumulador da soma e não estragar o S com isso.
O bloco principal
10 FOR I = 1 TO 200 20 READ N$ 30 GOSUB 10000 40 GOSUB 11000 50 GOSUB 12000 60 IF C = 0 AND A = 0 AND L = 1 THEN Q = Q + 1 70 NEXT 80 PRINT Q 90 END
Só temos um problema - de onde virão os 200 números? O comando READ, na linha 20, lê um valor de uma série de dados literais embutidos no código. Assim, adicionamos uma série de linhas a partir da linha 1000, cada uma com um comando DATA e uma série de strings. Montamos essa linha com um pouco de mágica de copy e paste e busca e troca.
Sim, eu poderia ter pulado os testes depois do primeiro eliminar o número, assim como ter começado com o teste da linha 12000, que é mais simples e rápido. Os algorítmos poderiam ser melhores também e eu poderia ter usado variáveis inteiras onde possível para que os programas rodassem mais rápido.
São 40 linhas com essa cara:
1000 REM Os numeros que precisamos filtrar 1010 DATA "214966", "215739", "220686", "225051", "225123" ... 1400 DATA "715315", "720200", "720202", "720568", "720576"
Quando rodamos o programa, temos a resposta esperada (já fizemos isso algumas vezes, afinal).


TRS-80 e Apple II concordam. 61 parece um bom número.
Isso era mesmo necessário?
Não. Eu não precisava ter feito isso nem mesmo uma vez. A primeira eu fiz porque achei as perguntas interessantes. Muitas e muitas vezes eu já entrevistei pessoas incapazes de escrever um programa de 5 linhas sem ajuda de um Google e, francamente, estou tentado a propor testes formais antes mesmo de um humano colocar os olhos em um currículo. O em Clojure foi motivado pelo contorcionismo sintático de expressar um algoritmo em um cruzamento de Ruby e JavaScript. Esse último veio pelo meu interesse em emuladores, pelo meu interesse em computadores antigos e por eu achar que aprender a programar com um computador de 8 bits é divertido. A simplicidade desses computadores facilita ao novato entender, direito, tudo o que acontece dentro deles nem. Não há compiladores cuidando de você e otimizando código ineficiente. Não há milhares de linhas de código de um kernel distribuindo tempo do processador por dezenas de processos. Tudo é bem simples e acontece do jeito que você mandou.
E, na hora de aprender, simples é bom.
Acho que o próximo precisa ser em FORTH. Vou começar a procurar um dialeto legal pra brincar.
E quanto a você?
Se você quiser brincar com um BASIC antigo, eu recomendo que comece lendo os manuais. Manuais do Apple II e do TRS-80 são fáceis de achar. Outra coisa: eu tomei cuidado de escrever esses programas de modo a eles serem portáteis - você pode usá-los em seu Prológica, Microdigital, ou Unitron. Deve poder rodá-los no seu Atari XL ou no seu Commodore 64. Não testei em todos.
Se você achar a brincadeira (é uma brincadeira - ninguém vai pagar vocë por saber programar um computador de 30 anos de idade) legal, compre um computador antigo e cuide dele. Limpe, conserte. Essas máquinas não vão durar para sempre e marcam o momento importante que essa tecnologia deu: quando deixou de ser aquela máquina que vivia fechada em uma sala e passou a ser aquela que tínhamos em casa. Como disse um especialista da Christies sobre o Apple I que foi leiloado esses dias, "é um pedaço de plástico verde que mudou nossas vidas".
Precisamos cuidar deles.
Mais uma coisa: não me escapou o fato de que esses dois BASICs que eu usei são produtos da Microsoft. Ela fazia coisas bem legais nos anos 70.